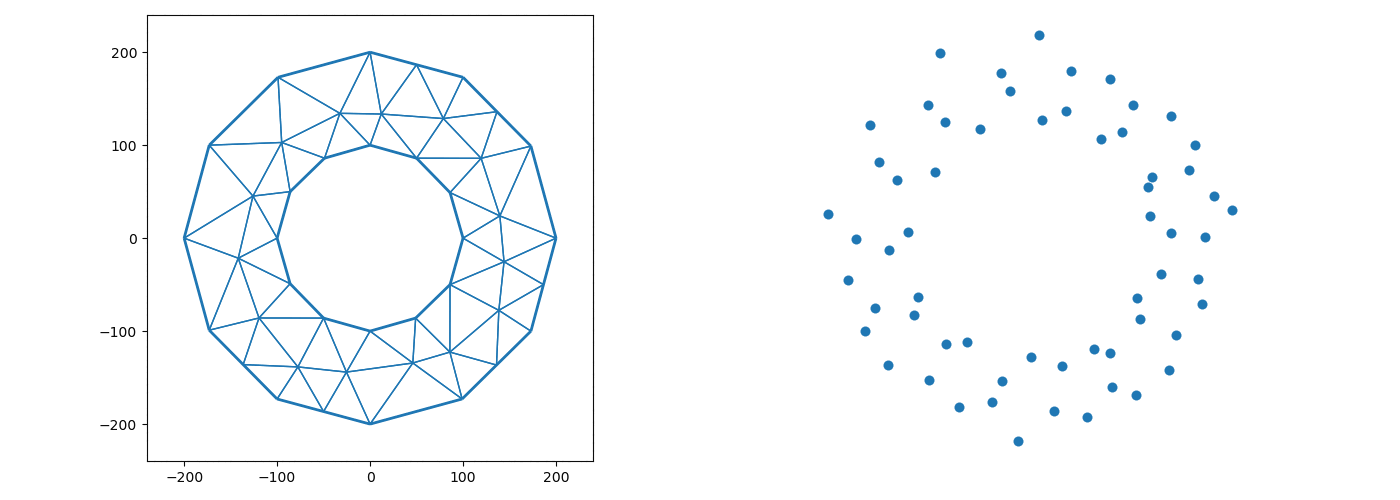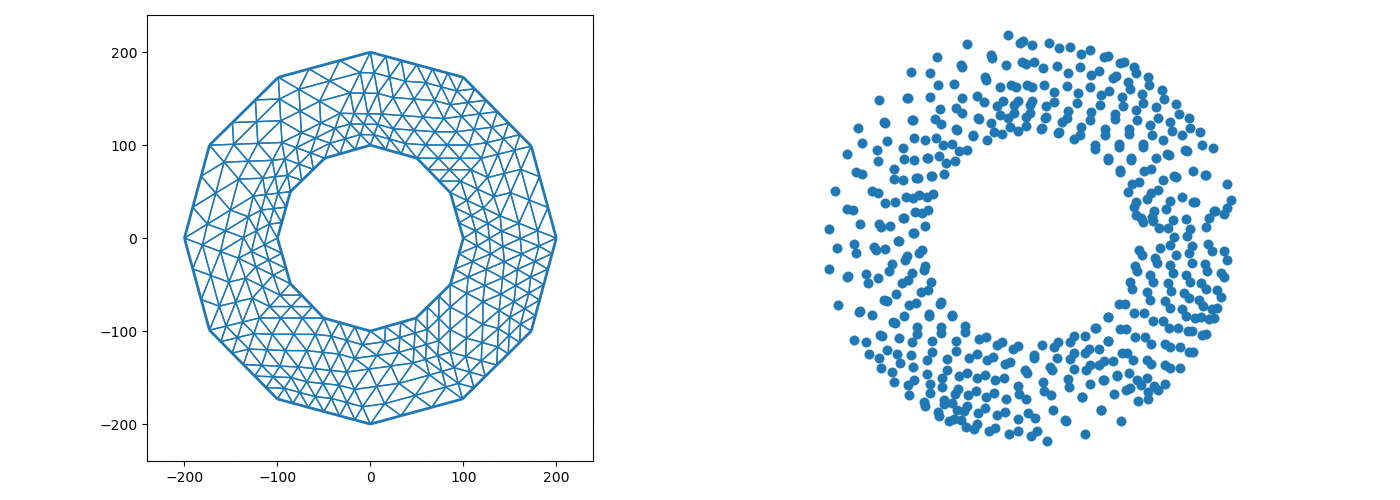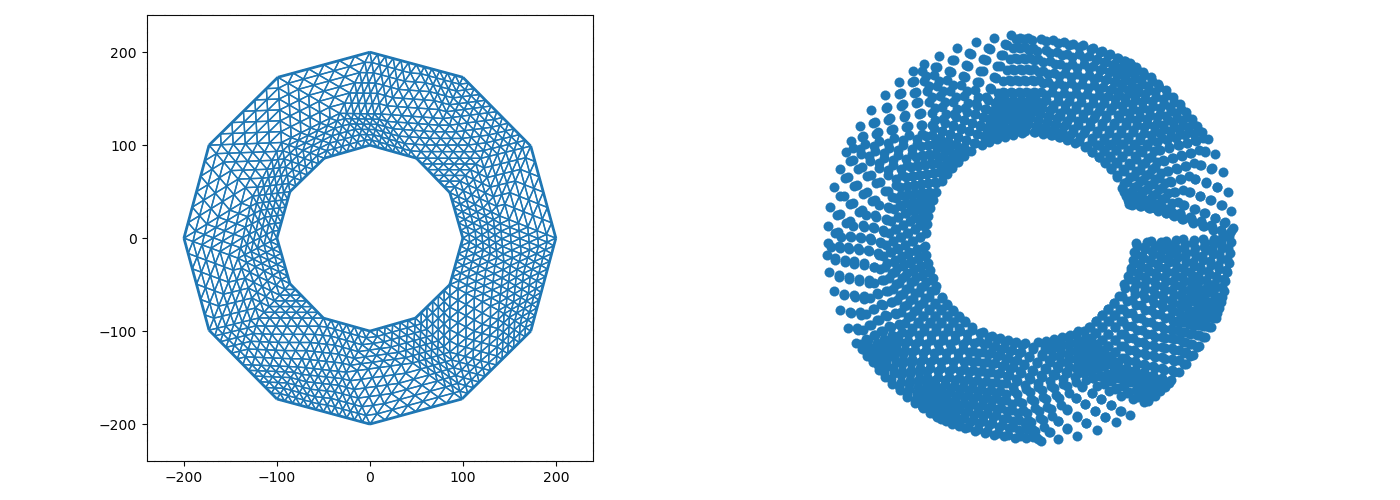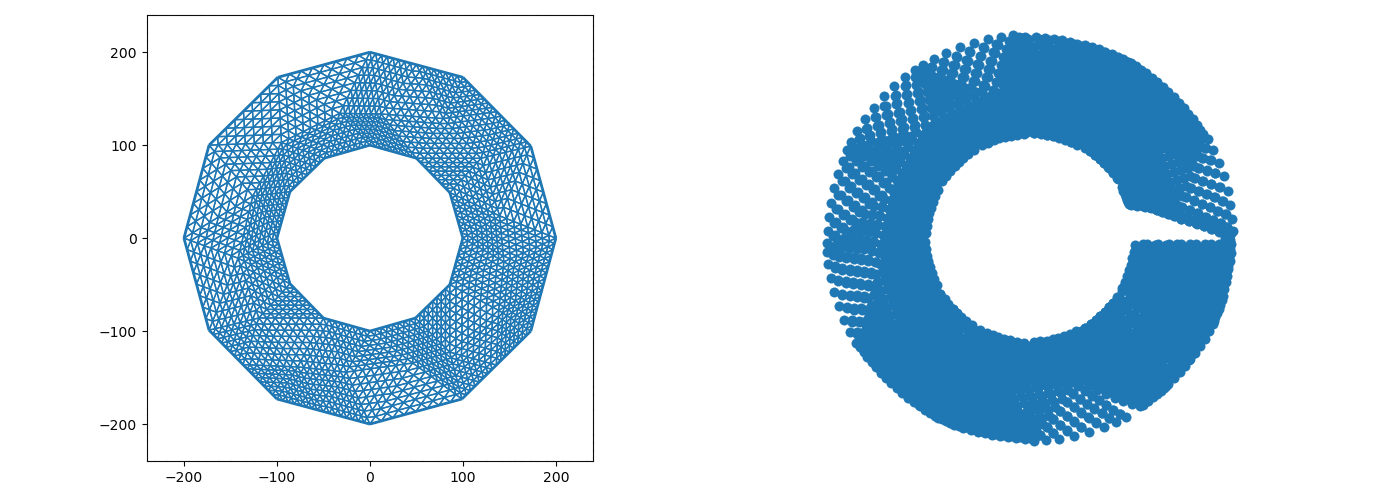
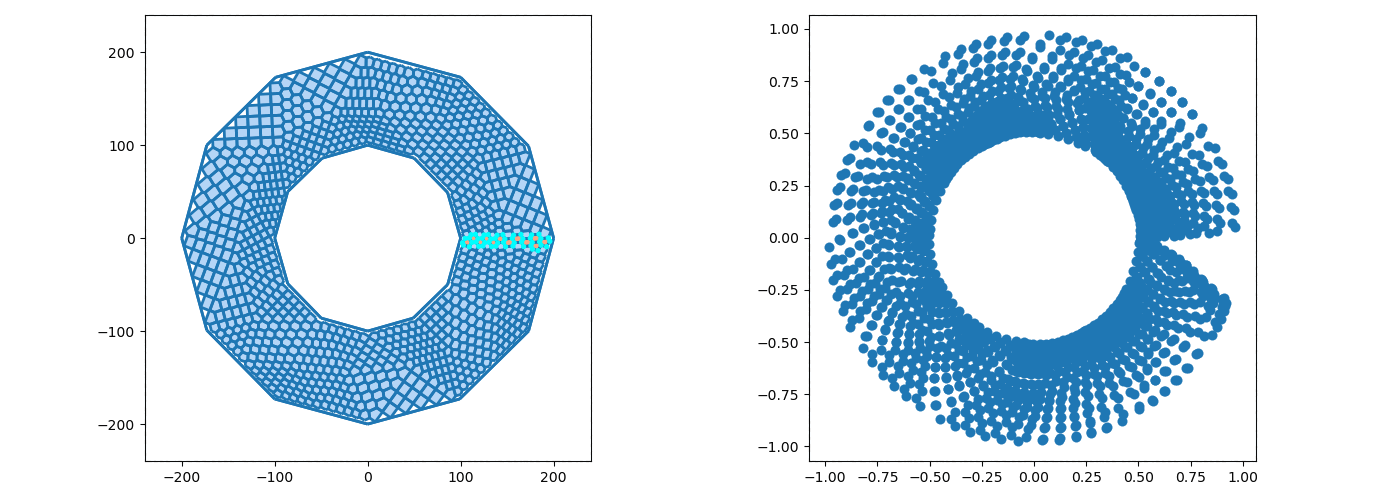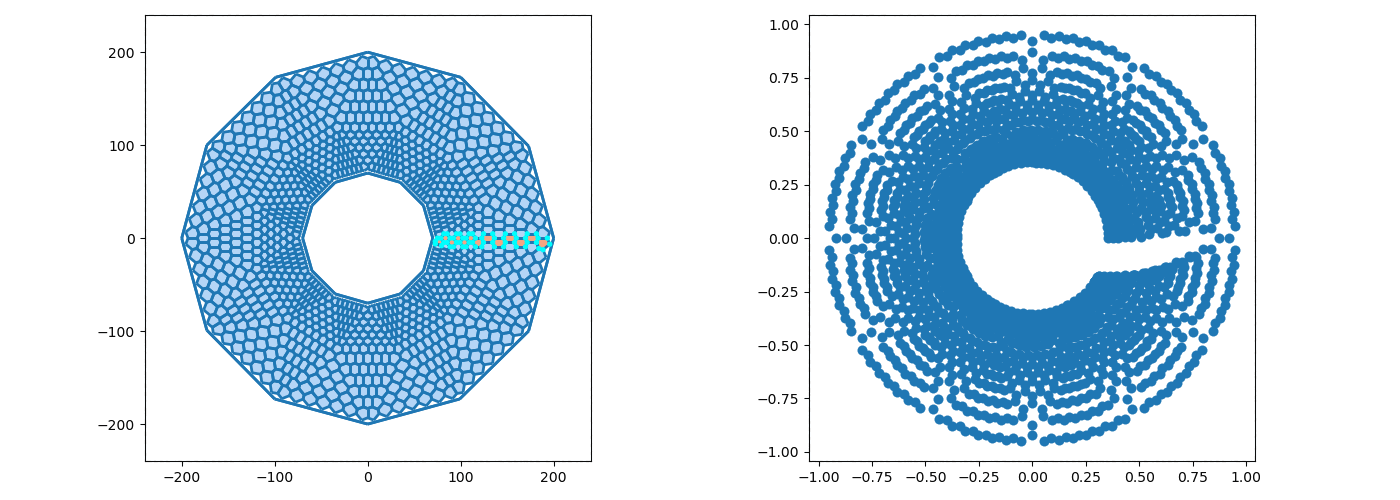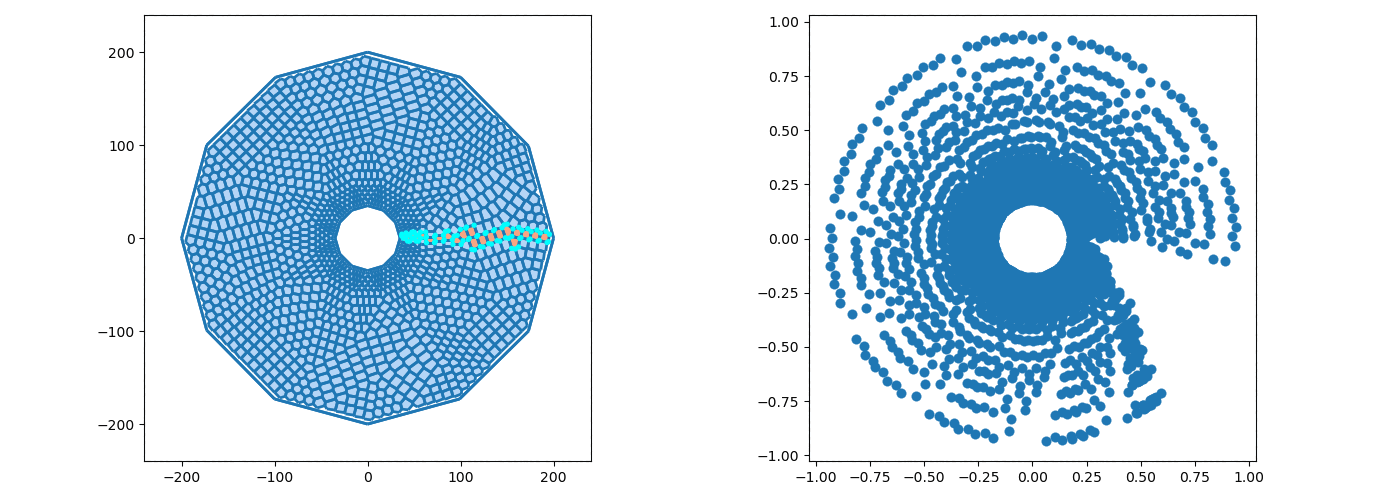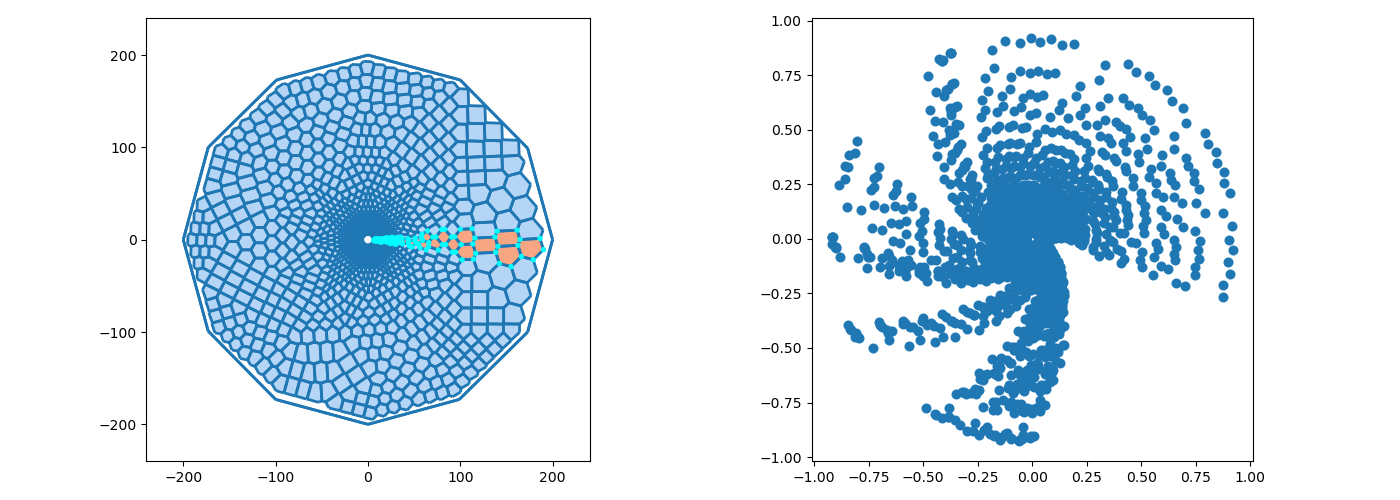
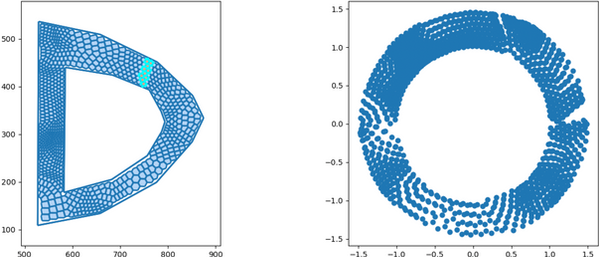
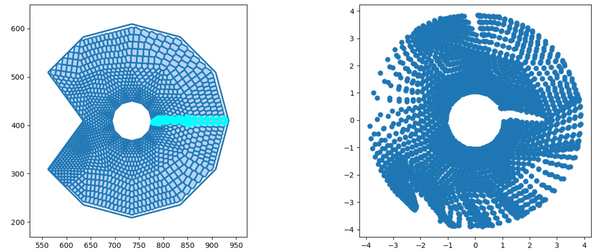
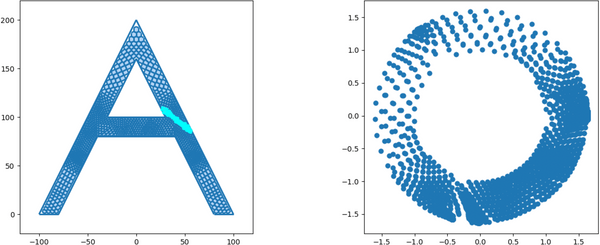
The graphics samples below were obtained by programs written by Dr. Erik Perkerson and myself. Joshua Konfrst created a GUI supporting this project. The project which aims to obtain effective version of uniformization theorems for planar domains and closed surfaces, relies heavily on PDEs (Boundary Value Problems in particular) and their approximation in Sobolev spaces (which turn out to be of fractional dimension in the applications). There are substantial new ingredients, beyond the PDEs theory, stemming from my work. This is explained in paper #29 on my Papers page.
In addition to obtaining explicit uniformization mapping of planar annuli, these programs helped me understand the behavior of piecewise linear singular level curves of discrete harmonic functions which come up in my research revolving in and around uniformization theorems of connected planar Jordan domains. A working version, for the case of an annulus, is posted on GitHub as Koebe-py. Koebe was the first to consider such questions, however, our methods are different. Most of the code is written in python, the parts which involve Julia and C (see below) are specific for the creation and refinement of acute triangulations.
The new algorithms implemented in the above mentioned programs are based on the mathematical analysis in paper #25 on my Papers page (see also #23 with H.R. Arabnia and T.R. Taha as well as #26 & #29 with E. Perkerson). Note that the programs are making an essential usage of the C program aCute (please write me if you wish to see more details) by creating acute triangulations of planar polygonal domains.
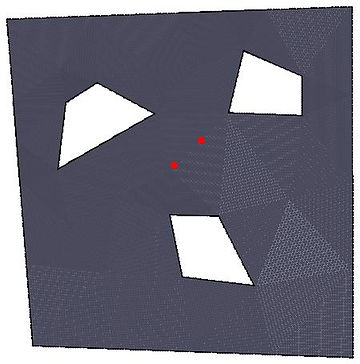
The uniformization of the second group is based on this decomposition (under writing and coding development).